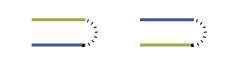
As you’ve seen, a nice problem in combinatorics is to list the number of ways to fold a strip of n stamps into a stack one stamp wide and n stamps tall. For example, if the stamps are different, two stamps can be folded in two ways:
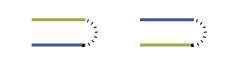
But if the stamps are blank, there’s really only one shape:
Likewise, three distinct stamps can be folded in six ways:
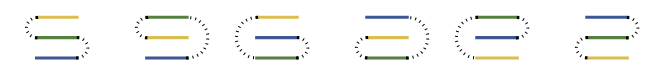
But there are only two basic shapes: the first labeled folding is the same as the last one upside down, and the second one is the same as the next three flipped horizontally or vertically or both:
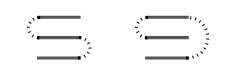
For four stamps, five basic shapes:

Five stamps, fourteen shapes:
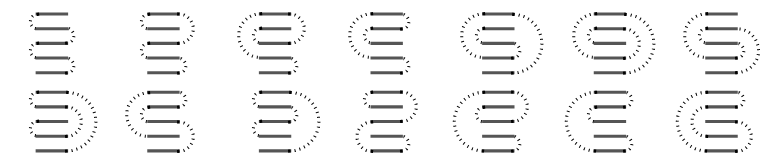
There doesn’t seem to be a closed-form formula for computing these counts, either. The first few terms look like the Catalan numbers, but larger numbers don’t match up; see OEIS A001011.
For a 2×2 sheet of stamps, there are 8 distinct foldings, but they’re all the same shape.
If you kind of liked this, you’ll kind of love labeled stamp foldings and map foldings.
See Martin Gardner, Wheels, Life and Other Mathematical Amusements, pp. 60–61, 1983.
Figures created with Mathematica 7.
© 2011–2025 Robert Dickau. All rights reserved, no responsibilities accepted.
[ home ] || [ 2013-05-27 ]
www.robertdickau.com/unlabeledfoldings.html