There are 2 self-avoiding (non-self-intersecting) paths from the southwest corner of a 1 × 1 grid to the northeast corner, using only steps north, east, south, or west):
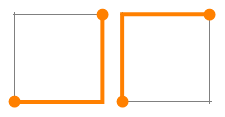
(In only this case, it turns out to be the same as the number of shortest paths.)
12 self-avoiding paths through a 2 × 2 grid:
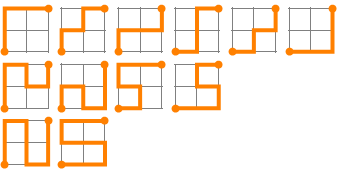
(Of these 12 paths: the first 6 take 4 steps; the next 4 paths take 6 steps; and the last 2 paths take 8 steps.)
184 paths through a 3 × 3 grid:

(Of these 184 paths: 20 of them take 6 steps; 36 take 8 steps; 48 take 10 steps; 48 take 12 steps; and 32 take 14 steps.)
This 2-D case is sequence A007764 in The On-Line Encyclopedia of Integer Sequences.
While we’re on the subject, there seem to be 18 self-avoiding paths through a 1 × 1 × 1 lattice:
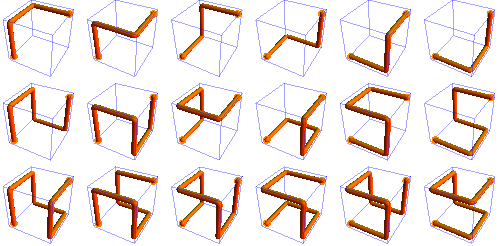
(Of these 18 paths: 6 of them take 3 steps; 6 paths take 5 steps; and 6 paths take 7 steps.)
156 paths through a 2 × 1 × 1 lattice:

There are 5,698 paths through a 2 × 2 × 1 lattice; here are some of the 30 shortest and 314 longest:
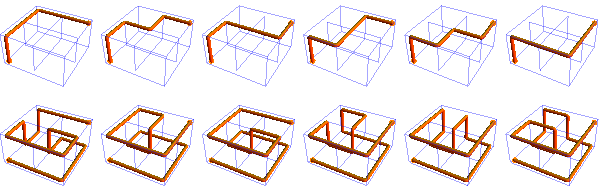
© 1998–2025 by Robert Dickau.
[ home ] || [ 2011-02-06 ]