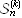 , and
, and
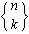 ,
where the first is by far the easiest to type.
,
where the first is by far the easiest to type.The Stirling numbers of the second kind, or Stirling partition numbers,
describe the number of ways a set with n elements can be partitioned into
k disjoint, non-empty subsets. Common notations are S(n, k),
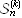 , and
, and
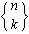 ,
where the first is by far the easiest to type.
,
where the first is by far the easiest to type.
For example, the set {A, B, C} can be partitioned into one subset (that is, not partitioned at all) in the following way, which means S(3, 1) = 1:
into two subsets in the following ways (making S(3, 2) = 3):
and into three subsets in the following way (S(3, 3) = 1):
Here are some diagrams representing the different ways the sets can be partitioned: a line connects elements in the same subset, and a point represents a singleton subset.
| S(3, 1): |  |
| S(3, 2): | 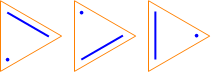 |
| S(3, 3): | 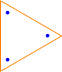 |
| S(4, 1): |  |
| S(4, 2): |  |
| S(4, 3): |  |
| S(4, 4): | 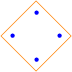 |
| S(5, 1): |  |
| S(5, 2): | 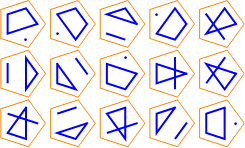 |
| S(5, 3): |  |
| S(5, 4): | 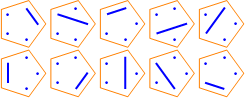 |
| S(5, 5): | 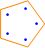 |
You’ll notice that S(n, 1) is always 1: there’s only one way to partition a set into one subset, which is to leave it alone.
You’ll also notice that S(n, n) is also always 1: there’s only one way to partition a set of length n into n subsets, each of length 1.
The Stirling numbers of the second kind also count numbers of ways to place nonattacking rooks on a triangular checkerboard. (Compare with the S(4, k) diagrams.)

(Does the game of checkers use rooks?)
The numbers can be computed recursively using the formula:
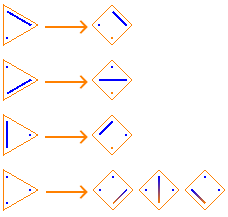
S(n, k) = S(n−1, k−1) + S(n−1, k)
The idea is that you can build up S(n, k) by:
For example, the following shows how to compute S(4, 3) by appending singleton {e}—represented by the orange dot at the bottom of each square—to each of the three S(3, 2) partitions, plus appending element e to each of the three S(3, 3) subsets:
The sums of the Stirling numbers of the second kind,
![Sum[StirlingS2[n, k], {k, 1, n}]](bellformula.png)
are called the Bell numbers.
About the checkerboard interpretation, see M. B. Wells, Elements of Combinatorial Computing, Oxford: Pergamon Press, 1971 p. 185.
Designed and rendered using Mathematica 3.0 and 7.0.
© 1996–2026 by Robert Dickau.
[ home ] || [ 2011-02-06 ]