The number of paths through a lattice given various restrictions—such as in which directions steps are allowed and what boundaries the path may not cross—describe many famous sequences of numbers. Here, the lattice paths start in the leftmost corner and continue to the rightmost corner.
The most familiar is surely the collection of paths from the beginning to end along the lattice lines, with steps (in this orientation) either northeast or southeast. There are two paths through a 1×1 lattice:
Six paths through a 2×2 lattice:

20 paths through a 3×3 lattice:

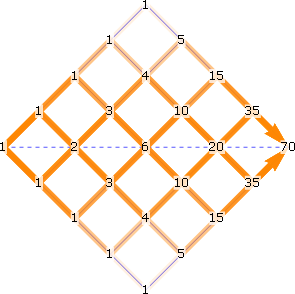
70 paths through a 4×4 lattice:

You can count the paths through these lattices by adding together the numbers of paths to each point in the lattice. There’s only one way to start at the leftmost point, so mark that point with a 1. Next, you can take a step northeast or a step southeast, with only one way to get to each of these points, so mark each of those with a 1. After that, you can get to the second point on the dotted line in two ways: NE-then-SE, or SE-then-NE. Continuing this way, you see that each of the points is described by the binomial coefficients, and the sequence of path counts for lattices of different sizes is 1, 2, 6, 20, 70, …, also known as the central binomial coefficients [OEIS A000984].
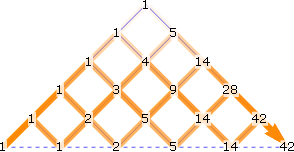
Now, if we change the rules so that a path can’t go below the dashed line connecting the start and end points, the path counts change, of course, but they’re not just half of the previous counts. One path through the top half of a 1×1 lattice:
Two paths through the top half of a 2×2 lattice:
Five paths through the top half of a 3×3 lattice:
We can again add the numbers of paths to each point. The sequence of path counts for lattices of different sizes is 1, 1, 2, 5, 14, 42, …, also known as the Catalan numbers [OEIS A000108].
If we do the same thing as the first lattice except for allowing steps east in addition to northeast and southeast, the path counts increase. For example, there are now three paths through a 1×1 lattice:
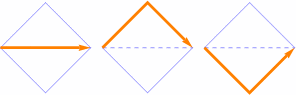
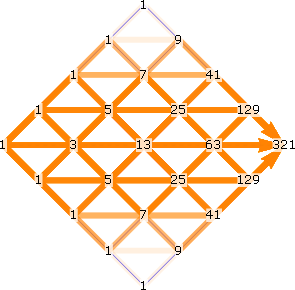
13 paths through a 2×2 lattice:
And 63 paths through a 3×3 lattice:

The path counts 1, 3, 13, 63, 321, …, are called the central Delannoy numbers [OEIS A001850].
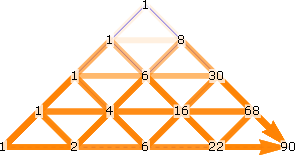
Likewise, if we restrict the paths to the upper half of the grid, we see different counts. Two paths through a 1×1 lattice:
Six paths through a 2×2 lattice:
22 paths through a 3×3 lattice:

The path counts for this arrangement, 1, 2, 6, 22, 90, 394, …, are called the Schröder numbers [OEIS A006318].
You can also extend the general idea to more dimensions—see 3-D, 4-D, and 5-D versions of the same idea—and to different rules—see for example Motzkin numbers.
© 1998–2026 by Robert Dickau.
[ home ] || [ 2011-05-22 ]