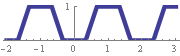
The Schoenberg curve is a fractal plane-filling curve, similar to the Peano, Hilbert, Moore, Lebesgue, and Wunderlich curves. The definition of the Schoenberg curve begins with a piecewise sawtooth-like function whose value falls between 0 and 1.

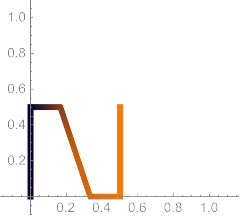
The curve is defined parametrically using sums of scaled copies of the original function. The first iteration is a one-half scale copy of the sawtooth function, beginning at the point (0, 0) and ending at (1/2, 1/2).
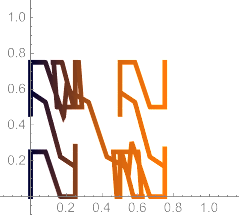
The second iteration adds a one-quarter scale copy to the previous copy, ending at (3/4, 3/4).
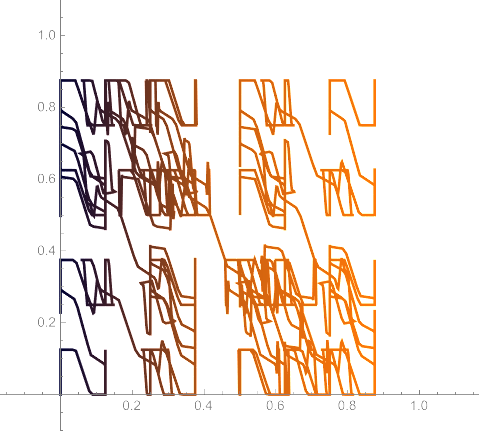
Each iteration spans more of the unit square. In its limit, the Schoenberg curve touches every point in the unit square.
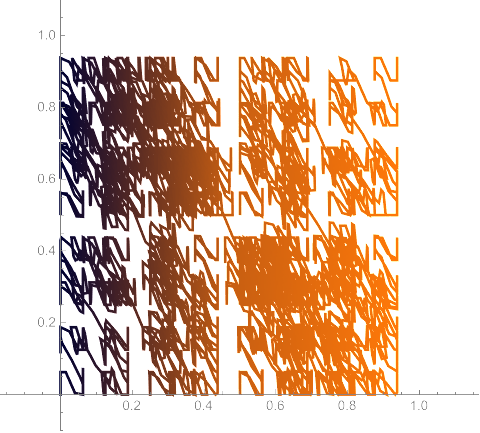
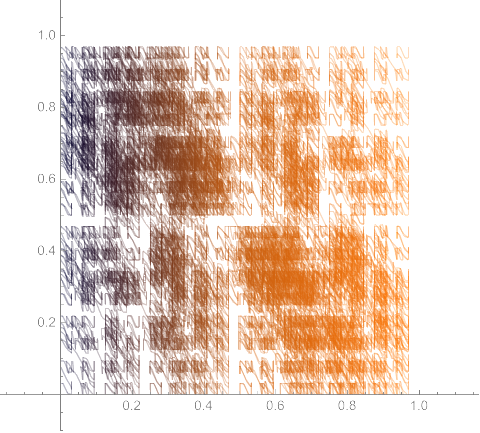
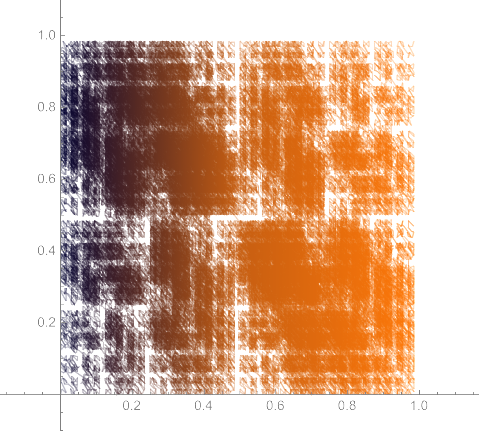
Same idea in 3-D, for filling the unit cube:
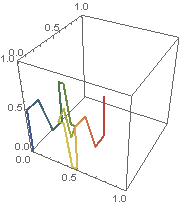
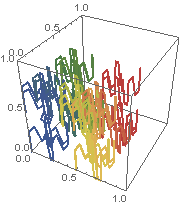
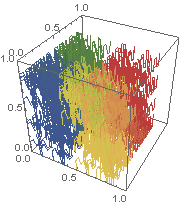
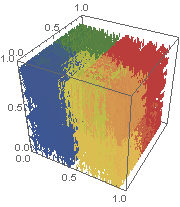
See I. J. Schoenberg and C. de Boor (ed.), “On the Peano Curve of Lebesgue”, in I. J. Schoenberg: Selected Papers Vol. 1, Boston: Birkhäuser, 1988.
Designed and rendered using Mathematica 7.0, 10.0, and 14.0.
© 2010–2025 by Robert Dickau.
[ home ] || [ 2024-02-18 ]
www.robertdickau.com/schoenberg.html